Exploring Optimization: A Guide to Iterative Local Search (ILS) |

To view a visualization of ILS (and Tabu Search) in action: AlgoScope

Many real-world problems, from logistics to scheduling, involve finding the best possible solution from a vast number of possibilities. These are known as optimization problems. While finding the absolute best solution (the global optimum) can be computationally expensive or even impossible for complex scenarios, metaheuristic algorithms offer powerful strategies to find very good solutions in a reasonable amount of time.

In this post, we’ll explore a popular metaheuristic: Iterative Local Search (ILS). We’ll break down its core concepts, look at pseudocode, and see a simple Python implementation.

Iterative Local Search (ILS) Simply Explained.

Imagine you’re climbing hills blindfolded. You start at a random spot and try to find the highest point. You take steps upwards until you can’t climb any higher. At this point, you’ve reached a ‘local’ hilltop (a local optimum). However, you have no way of knowing if there are other, higher hills nearby or far away. This initial process is a ‘local search.’

To find a potentially higher hill (a better solution), Iterative Local Search introduces a “perturbation” step. You essentially take a ‘jump’ to a different, somewhat random coordinate, hoping to land in a new region where another local search might lead you to an even higher hilltop. You repeat this process of local search and perturbation many times to explore a significant portion of the solution space.

ILS Pseudocode

The general structure of an ILS algorithm looks like this:

function ILS():
    solution = GenerateInitialSolution()
    best_solution = LocalSearch(solution)

    while not TimeLimitReached():
        new_solution = Perturb(best_solution)
        new_solution = LocalSearch(new_solution)

        if Cost(new_solution) < Cost(best_solution):
            best_solution = new_solution

    return best_solution

Where:

GenerateIntialialSolution() makes a random starting solution. Alternatively we could also leverage other heuristic start such as based on some simple rules (greedy, random permutation, etc.). It doesn’t guarantee optimality, but it helps the algorithm expore various parts of the solution space.
LocalSearch(solution) improves the solutin using simple, local changes. In Travel Sales Man (TSP), it does so by swapping the cities; in JobShop Problem, it reassigns jobs.
Cost(solution) computes how good the solution is (e.g. total path length or machine workload).
TimeLimitReached() is a contraint where the algorithm is allowed to loop a fixed number of iterations or time.

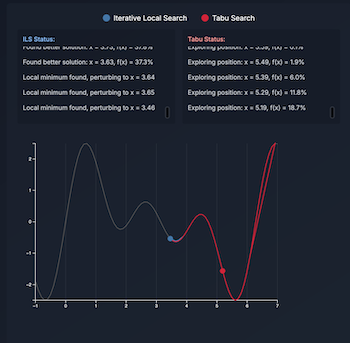
Now let’s look at a possible implementation of ILS in Python, where our objective function is:

\[f(x) = - (x - 3)^2 + 9\]

Visually it looks like this:

f(x)
|                       *
|                  *       *
|              *             *
|          *                   *
|      *                         *
|  *                               *
    +------------------------------------→ x
    1      2      3      4      5

We picked this simple parabola function because it has a single peak at x=3. It is thus easy to visualize how the search algorithm works we moving across it.

So based on the algorithm we have the following:

Start at a random point (say x = 0.8).
Perform greedy hill-climbing until no more improvement.
If stuck, make a random jump (perturbation).
Repeat until time budget expires.

A python implementation is:

import random

def f(x):
    return - (x - 3) ** 2 + 9  # Peak at x = 3

def tabu_search(start, steps=100, tabu_size=5):
    current = start
    best = start
    tabu_list = []

    for _ in range(steps):
        # Generate neighbors
        neighbors = [current + delta for delta in [-0.2, -0.1, 0.1, 0.2]]
        # Filter out tabu moves
        neighbors = [x for x in neighbors if round(x, 4) not in tabu_list]

        if not neighbors:
            break  # stuck — all neighbors are tabu

        # Choose best neighbor
        next_x = max(neighbors, key=f)

        # Update tabu list
        tabu_list.append(round(current, 4))
        if len(tabu_list) > tabu_size:
            tabu_list.pop(0)

        # Update current and best
        current = next_x
        if f(current) > f(best):
            best = current

    return best, f(best)

# Run Tabu Search
x0 = random.uniform(0, 6)
x_found, fx = tabu_search(x0)
print(f"Tabu Search found maximum at x = {x_found:.3f}, f(x) = {fx:.3f}")
# Tabu Search found maximum at x = 2.999, f(x) = 9.000

Example 1: Job Scheduling

Job scheduling, sometime also known as JobShop problem is a classic usage of ILS. Suppose you have 5 machines and 20 jobs. Each job has to be assigned to a machine, and each takes a different amount of time depending on the machine. The goal is to assign jobs to machines so that the total time to finish all jobs is minimized.

The algorithm:

Start with a random assignment of jobs to machines.
Greedily reassign jobs to reduce the total time (e.g., move job from overloaded machine to underloaded one).
When stuck in a local minimum, randomly swap or reassign a few jobs.
Repeat steps 2–3 for a while.

Example 2: Travel Salesman Problem (TSP)

The classic NP-hard problem TSP says that a salesman needs to visit a certain number of citities, and exactly once every city (no repeat visit). Then he must return to the city where he started at. The goal is to find the shortest possible trip.

Start with a random city order (tour).
Use a local search like 2-opt (swap two edges to improve the path).
Once stuck (no improvement), shuffle a few cities to create a new starting point.
Repeat.